Scratch TD 2Probabilité
Dans cette partie, nous allons utiliser le générateur aléatoire de Scratch dans deux situations :
- Le paradoxe des deux enfants
- La méthode de Monté-Carlo
Exercice 1
Paradoxe des deux enfants
En théorie des probabilités, le paradoxe des deux enfants consiste à estimer le sexe d'un enfant parmi deux à partir de l'observation de l'autre, exemple-type d'inférence bayésienne.
M. Smith a deux enfants. Au moins l'un des deux est un fille.
La probabilité que les deux enfants soient des filles est
Modélisation de la situation
La simultation de l'expérience
Pour simuler l'expérience, on représentera les garçons par le nombre 1 et les filles par le nombre 2. Pour connaître la composition de la famille, nous allons regarder le produit:
On a la correspondance suivante :
- Garçon / Garçon = 1 (1*1)
- Garçon / Fille ou Fille / Garçon = 2 (1*2 ou 2*1)
- Fille / Fille = 4 (2*2)
Créer un bloc, nommé
La répétition de l'expérience
Pour répéter l'expérience, on créera deux compteurs qu'on initialisera à 0.
exp : compteur qui retient le nombre de tirages modélisant correctement la situation (c'est à dire qui contient au moins une fille )ff : compteur qui retient le nombre de tirage représentant la situation Fille - Fille
Répéter 5000 fois l'expérience tirage en incrementant pour chaque tirage les compteurs approrpiés.
Ajouter l'affichage de la proportion du nombre de tirages Fille-Fille sur le nombre de tirages ayant correctement représenté la situation.
La proportion du nombre de tirages Fille-Fille sur le nombre de tirages ayant correctement représenté la situation est proche de
Exercice 2
Monté Carlos
La méthode de Monté-Carlos est une méthode algorithmique qui permet d'approchée une valeur numérique par le biais de processus aléatoire. On la retrouve souvent dans le calcul des aires.
Pour l'approximation d'une surface, la méthode consiste à prendre des points au hasard sur une surface d'aire connue et de voir si ces points appartienne à la surface recherché.
A la façon Mondrian
Dans ce tableau inspiré du peintre Piet Mondrian, on veut déterminer quelle surface colorée (jaune, bleue ou rouge) est la plus grande.
D'après vous quelle est la surface la plus grande ?
La simultation de l'expérience
Pour simuler cette expérience on va placer au hasard, des points et regarder sur quelle coulleur il touche.
- Télécharger le tableau ici
- Puis place en tant que fond d'écran, à l'aide du menu

- Créer les compteurs
bleu ,rouge ,jaune initialisés à 0. - Choisir le sprite
 et lui donner une taille de 20 pixels.
et lui donner une taille de 20 pixels. - Pour ce sprite, créer un bloc tirage qui : -- le positionne aléatoirement à l'aide de l'instruction
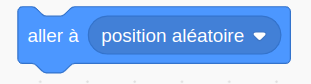 (menu
(menu mouvement ) -- incrémente les compteurs si nécessaire. On detectera la couleur à l'aide de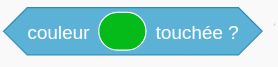 (menu
(menu capteur )
La fenêtre de scratch fait 480px par 360px. Le nombre total de pixels occupés par les surfaces bleues est d'environ
